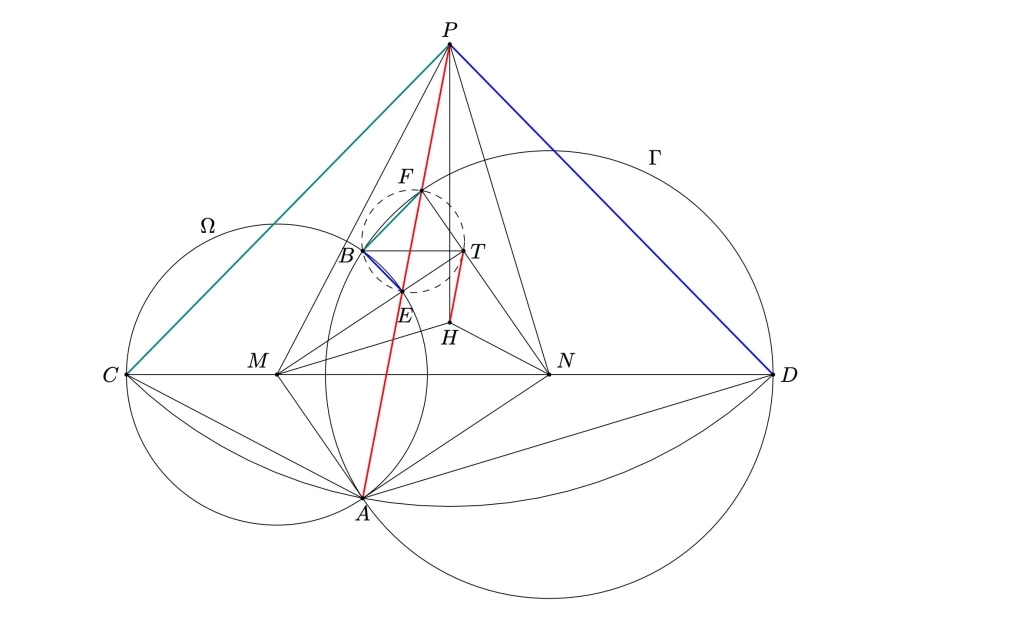
 |
| Hình vẽ của một trong 9 cách giải bài Hình học của thầy Trần Quang Hùng |
Bài toán của thầy là câu 2, thuộc lĩnh vực Hình học, được đưa ra trong ngày thi đầu tiên của IMO 2025, tổ chức tại Australia từ 11-22/7/2025.
Nội dung bài toán như sau:
"Let Ω and Γ be circles with centres M and N, respectively, such that the radius of Ω is less than the radius of Γ. Suppose Ω and Γ intersect at two distinct points A and B. Line MN intersects Ω at C and Γ at D, so that C, M, N, D lie on MN in that order. Let P be the circumcentre of triangle ACD. Line AP meets Ω again at E≠A and meets Γ again at F≠A. Let H be the orthocentre of triangle PMN.
Prove that the line through H parallel to AP is tangent to the circumcircle of triangle BEF.
(The orthocenter of a triangle is the point of intersection of its altitudes)".
Bản dịch:
"Cho các đường tròn Ω và Γ có tâm tương ứng là M và N sao cho bán kính của Ω nhỏ hơn bán kính của Γ. Giả sử các đường tròn Ω và Γ cắt nhau tại các điểm phân biệt A và B. Đường thẳng MN cắt Ω tại điểm C và cắt Γ tại điểm D, sao cho thứ tự các điểm trên đường thẳng đó lần lượt là C, M, N và D. Gọi P là tâm đường tròn ngoại tiếp tam giác ACD. Đường thẳng AP cắt lại Ω tại điểm E ≠ A. Đường thẳng AP cắt lại Γ tại điểm F ≠ A. Gọi H là trực tâm của tam giác PMN.
Chứng minh rằng đường thẳng đi qua H và song song với AP tiếp xúc với đường tròn ngoại tiếp tam giác BEF.
(Trực tâm của một tam giác là giao điểm của các đường cao của nó)".
Đây là một dấu mốc đáng tự hào không chỉ đối với cá nhân thầy Hùng mà còn với toàn thể đội ngũ giáo viên giảng dạy và học sinh chuyên Toán Việt Nam, đặc biệt là tại Trường THPT chuyên Khoa học Tự nhiên – nơi có truyền thống đào tạo học sinh giỏi Toán hàng đầu cả nước.
Nội dung bài toán được đánh giá là “đẹp, ngắn gọn, hiện đại và tư duy sâu sắc”, yêu cầu thí sinh chứng minh tính chất tiếp xúc đặc biệt giữa một đường thẳng và một đường tròn trong tam giác có trực tâm. Đây cũng là bài toán hình duy nhất trong đề IMO năm nay, và là bài toán của Việt Nam đầu tiên được chọn vào đề thi chính thức sau gần 40 năm.
 |
| Thầy Trần Quang Hùng (trái) cùng thầy Nguyễn Chu Gia Vượng (trưởng đoàn) và các học sinh dự IMO 2025. |
Thầy Trần Quang Hùng cho biết bài toán được hình thành trong quá trình nghiên cứu, giảng dạy và huấn luyện học sinh giỏi. Về quy trình, khoảng bốn tháng trước kỳ thi, trưởng đoàn của mỗi nước sẽ tập hợp các bài toán đề nghị, tác giả không nhất thiết là người trong đoàn mà chỉ cần là người của nước mình, rồi gửi ban chọn đề của nước đăng cai. Nước đăng cai kỳ thi sẽ chọn khoảng 30 bài, đưa vào danh sách rút gọn (IMO short list). Vài ngày trước khi kỳ thi diễn ra, các trưởng đoàn bỏ phiếu để chọn ra 6 bài chính thức.
PGS.TS Nguyễn Vũ Lương, Chủ tịch Hội đồng Khoa học và Đào tạo của Trường THPT chuyên Khoa học Tự nhiên, đánh giá: “Bài toán có cấu trúc hình học đơn giản, ngắn gọn nhưng đòi hỏi thí sinh phải vận dụng nhiều kiến thức tổng hợp và tư duy hình học sắc bén. Đây là thành công xứng đáng cho tâm huyết và năng lực chuyên môn của thầy Trần Quang Hùng.”
Tính đến nay, đây là lần thứ tư Việt Nam có bài toán được chọn vào đề thi chính thức của IMO, sau các năm 1977, 1982 và 1987. Thành tích này không chỉ ghi dấu ấn học thuật của các nhà giáo Việt Nam trên đấu trường quốc tế, mà còn là minh chứng cho chất lượng đào tạo, nghiên cứu và phát triển tài năng trẻ mà ĐHQGHN, trong đó có Trường THPT chuyên Khoa học Tự nhiên, đang không ngừng vun đắp.
